流固耦合问题，涉及到非稳态的流体流动与结构运动之间的相互耦合，在许多工程学领域，以及科学领域（例如生命医学）中都会遇到。而对于浸没在流动流体中的柔性结构发生自激振动的流固耦合问题，由于这种振动对结构和流体特性非常敏感，所以很难预测。随着计算机能力的不断提高，这些复杂的流固耦合问题引起了越来越多的计算力学研究者的兴趣。今天给大家带来一个自激振动问题双向流固耦合的仿真案例。这个案例最大的亮点就是，仅用到了STAR-CCM+这一款工具，就同时解决了流体、结构的耦合问题。可能有的CFDer对于STAR-CCM+结构有限元求解器还不甚了解。这个列表是其结构有限元求解器的几个基本功能：

　　•     集成环境中即可完成从CAD 到求解、后处理的工作流程；

　　•       一阶和二阶3D 六面体、四面体、楔形体和棱锥体单元；

　　•       静态、准静态和动态分析；

　　•       材料非线性和几何非线性；

　　•       各向同性、正交各向异性和各向异性、线性弹性以及超弹性材料；

　　•       表面和点的载荷和约束；

　　•       温度场的热应力；

　　仿真的实验对象，是验证柔性结构体在层流作用下，产生周期性变形、摆动的问题。该实验对结构的选择和实验条件有着非常严格的要求。实验要求主要基于五个方面：

　　•       自激振动现象是可以复现的；

　　•       结构的变形是二维平面的；

　　•       要有适当的振动频率；

　　•       明显的结构运动、位移；

　　•       线性结构材料；

　　经过了一段时间的测试后，最终的结构形式选定为，由厚度为0.04 mm的不锈钢薄板连接到直径为22 mm的铝制圆柱上,见下图(单位为mm)。在薄板的后缘处，放置了一个10 mm×4mm的矩形钢块。所有的结构都可以自由地绕着位于前端圆柱中心点的轴旋转。前端圆柱和后端钢块可以认为是刚性的。在测试过程中，薄板测得的杨氏模量为200 kN / mm2。结构的整体展向尺寸为177 mm。实验的雷诺数为500.

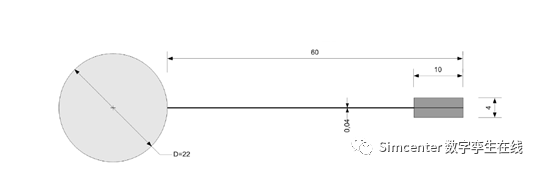
　　流固耦合模型设置

　　基于前面实验的几条假设，我们可以采用二维的计算域模型，用多面体网格离散流体计算域,并在流体域中固体表面添加棱柱层网格，以保证流固耦合交界面附近的网格质量。用四面体网格离散结构前端圆柱及后端钢块，用六面体网格离散结构中间柔性薄板。

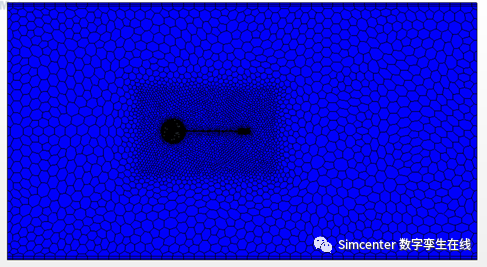
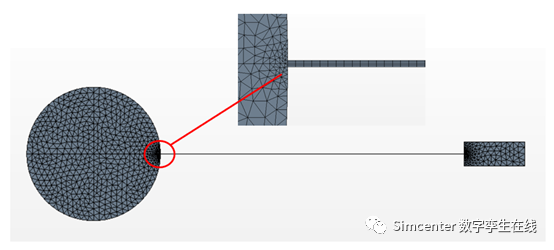
　　选取流体计算域模型，采用层流。

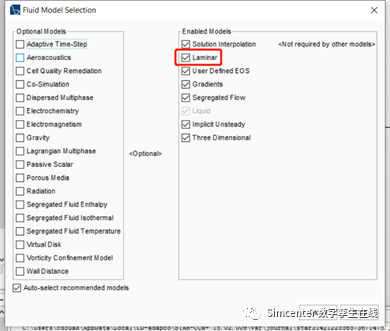
　　对于结构部分，当结构部件是装配体时，为了方便模型的设置。我们可以采用多体部件的方法，即将所有的固体零部件集中到一个计算域下进行设置。只需要根据输入零部件指定不同的材料属性即可。在物理模型选择中，我们同时考虑结构的大变形及流固耦合问题。

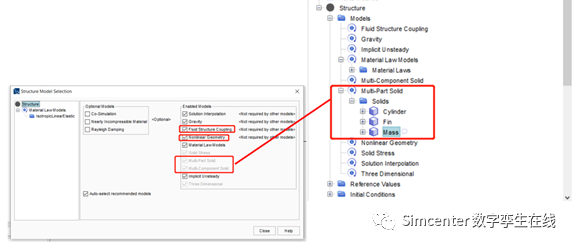
　　边界条件设置

　　对于固体圆柱、薄板及钢块，系统会自动添加描述三者接触关系的交界面。我们采用默认即可。默认的接触关系即为绑定，三者不会出现分离或相对运动。

　　对于固体域与流体域之间的流固耦合交界面，两个计算域采用的网格并不是共形的拓扑关系，我们把接触类型改为：映射接触。

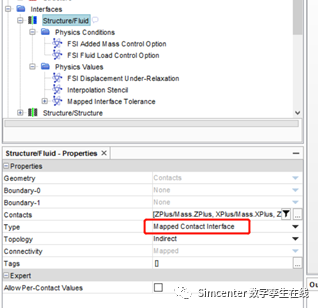
　　根据实验流体介质属性及工况，设置入口的流速为1.08m/s.出口为环境压力。考虑到流固耦合带来的流体边界变形，我们将所有流固耦合交界面边界的网格变形策略设置为：跟随固体应力变形。

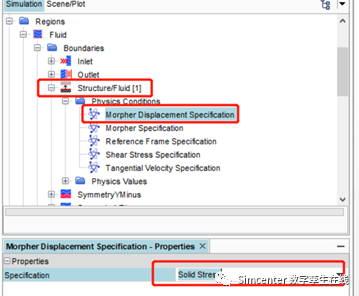
　　对于固体部分，按照实验方法，我们对圆柱中心添加固定点约束。其它非流固耦合交界面的固体表面，添加对称面约束条件，以限制固体在平面内运动和变形。

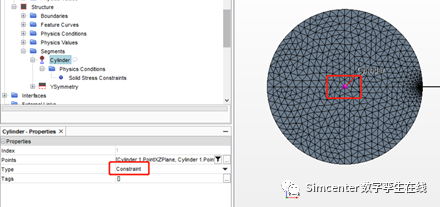
　　求解器及监测信号设置

　　我们将流体和结构的耦合方式更改为：双向。非稳态时间步长为0.001，离散格式为1阶。流体内迭代次数为20次，固体采用默认即可，计算时间为6s。

　　我们通过监测钢块上一点位移随时间的变化规律，判断流固耦合系统是否稳定：即呈现规律性的变化。

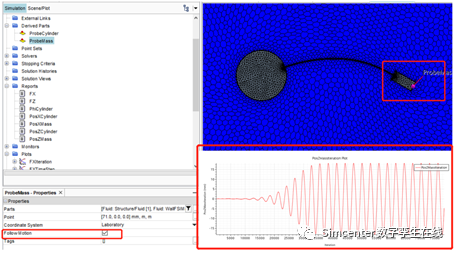
　　后处理

　　结构的运动模式主要以绕轴偏转振动为主，在雷诺数为500时，系统并且表现出来的振动特性为其第一固有频率（约6hz）的特征。下面上图为实验捕获的结构运动形态的图片。下面动画为仿真结果捕获的结构运动、变形过程。